What are Decimals?

A decimal is a numerical representation that expresses a whole number and its fractional part, separated by a decimal point. The digits to the left of the decimal point represent the whole number, while the digits to the right of the decimal point represent a fraction of the whole. Decimals are based on the base-10 system, where each place value represents a power of 10. For instance, the decimal number 25.47 can be broken down as 25 (whole number) and 0.47 (fractional part). The fractional part, in this case, signifies that the number is slightly less than 26. Decimals allow for precise representation of values between whole numbers, which is crucial in situations requiring accuracy, such as in science, engineering, and finance.

Decimals are particularly useful because they provide a more intuitive way to handle fractional numbers compared to fractions. For example, a fraction like 1/2 can also be expressed as the decimal 0.5. This form is often easier to understand and compute in many contexts, especially with calculators and computers. Decimals are universally used in measurements (like 3.75 meters), money (like $12.50), and other everyday contexts where exact values are important.

Why is it essential to learn Decimals?

Decimals are crucial for representing precise measurements in a wide range of contexts, from everyday activities to advanced scientific research. Many quantities in the real world are not whole numbers and often require fractional values to represent them accurately. For instance, when you measure lengths, weights, or time, the values often include decimals. A carpenter measuring wood for a project might need to cut a piece to 5.75 inches rather than simply 5 or 6 inches, and a doctor calculating a precise dosage for a medication might need to measure it in terms like 0.25 milligrams. Decimals allow for this level of precision, which is often essential for ensuring the accuracy and quality of results. Moreover, fields like engineering, astronomy, and finance rely heavily on decimals for precision. In engineering, even the slightest miscalculation could lead to faulty designs or unsafe structures, so engineers must use decimals to make precise calculations. Similarly, astronomers use decimals to calculate vast distances in space, and finance professionals use decimals to handle small differences in interest rates, prices, or profits. Whether in everyday tasks or high-stakes fields, learning about decimals helps ensure accuracy and enables people to solve real-world problems with precision.

Decimals offer a simpler, more standardized way to handle fractions, especially in comparison to the often complex operations involved with traditional fractions. Unlike fractions, which can have a variety of different numerators and denominators, decimals are all based on the powers of 10, making them easier to work with, especially when it comes to comparing, adding, subtracting, multiplying, or dividing numbers. For example, comparing 3/4 and 5/8 involves finding a common denominator, while comparing their decimal equivalents—0.75 and 0.625—is a straightforward process. Decimals also play a significant role in our digital world. Computers and calculators are designed to work with decimals rather than fractions, as the base-10 decimal system is inherently compatible with digital processing. This makes learning decimals particularly important in today’s technology-driven society. For instance, when working with spreadsheets, accounting software, or any digital tools, numbers are almost always represented as decimals. Understanding how decimals function helps in using these technologies effectively, simplifying tasks like financial calculations, data analysis, or programming.

Learning about decimals is essential for managing personal finances and enhancing financial literacy. Most financial transactions involve decimals, whether you’re dealing with prices, interest rates, taxes, or discounts. For example, when you purchase items at a store, the prices are often in decimal form, like $19.99 or $5.49, rather than whole numbers. Sales tax and discounts are also calculated as percentages, which involve decimals. Knowing how to work with decimals allows you to quickly calculate how much you need to pay, how much you’re saving, or how interest will affect your savings over time. In a more advanced context, understanding decimals is vital for making informed financial decisions, such as understanding interest rates on loans or savings accounts. For example, a mortgage rate might be 3.75%, and understanding this rate in decimal form allows you to calculate your monthly payments and the total interest paid over the life of the loan. Similarly, investment returns and stock prices are often expressed in decimal format, so learning about decimals empowers individuals to make smart decisions when managing investments, evaluating financial risks, or planning for long-term financial goals. Financial literacy, a key life skill, is deeply tied to the ability to understand and work with decimals effectively.

Place Values

Decimal Point and Place Value System

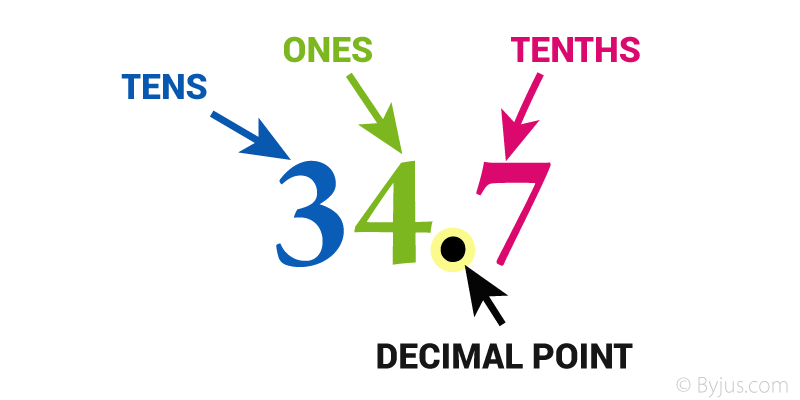
The decimal system is based on place values, where the position of each digit relative to the decimal point determines its value. The decimal point serves as a divider between the whole number and the fractional part of the number. To the left of the decimal point are the whole numbers (units, tens, hundreds, etc.), while to the right are fractional values like tenths, hundredths, and thousandths. Each place value is a power of 10. For example, in the number 123.456, the digits 1, 2, and 3 are in the hundreds, tens, and units places, respectively, while the digits after the decimal point, 4, 5, and 6, represent fractional values. The decimal point itself is crucial as it clearly indicates the transition from whole numbers to fractions, allowing us to express non-whole numbers in an organized way.

The place value system ensures that each digit has a specific and consistent meaning based on its location. This is what makes the decimal system so powerful and easy to understand. Each move to the left or right of the decimal point represents a multiplication or division by 10. For instance, moving one place to the left increases the value by 10 (e.g., from tenths to units), and moving one place to the right decreases the value by a factor of 10 (e.g., from tenths to hundredths). This systematic structure makes it easy to compare, add, or subtract decimals as well as to perform more complex operations like multiplication or division.

Place Values to the Right of the Decimal Point

The digits to the right of the decimal point represent fractional parts of a whole. The first digit immediately to the right is in the tenths place, which is 1/10 of the whole. This means that if you have a decimal like 0.5, the 5 in the tenths place represents 5 tenths, or half of 1. The second place to the right is the hundredths place, representing 1/100 of a whole. In a number like 0.25, the 2 represents 2 tenths and the 5 represents 5 hundredths, combining to give a value of 25 hundredths, or 25/100. Moving further to the right, the third place is the thousandths place, representing 1/1000, which allows for even more precise measurements and values. In the number 0.123, for example, the 1 is in the tenths place, the 2 in the hundredths place, and the 3 in the thousandths place, representing a very small fraction of 1.

Understanding these place values is important for accurate mathematical operations and problem-solving. For instance, when you perform addition or subtraction with decimals, you must align the decimal points to ensure that each digit is added or subtracted from its corresponding place value. If the place values are misaligned, the calculation will be incorrect. In practical situations, these small fractional values are vital in fields like science and engineering, where precise measurements are necessary. Even in everyday life, decimals play a role in pricing, weight measurements, and time, all of which involve careful attention to these smaller fractional parts.

Comparing Decimal Place Values

Comparing decimal place values involves looking at each digit from left to right, starting with the whole number portion and moving toward the fractional part. The farther to the left a digit is, the larger its value. For instance, in the numbers 45.67 and 45.72, both have the same whole number part (45), but to compare them, you must look at the decimal digits. Both have a 6 in the tenths place, but when you look at the hundredths place, the first number has a 7, and the second number has a 2. Since 7 hundredths is greater than 2 hundredths, 45.72 is larger than 45.67. This ability to compare decimals by examining place values is crucial in contexts like finances (e.g., comparing prices, interest rates) or measurements (e.g., comparing lengths or weights).

Additionally, understanding place values helps when rounding decimals. Rounding is often necessary when you don’t need or want to work with very small fractions. To round a decimal, you look at the place value immediately after the one to which you want to round. For example, to round 3.456 to the nearest hundredth, you look at the digit in the thousandths place (6). Since it is 5 or greater, you round the number up, making it 3.46. Being able to round decimals properly is essential for simplifying complex numbers in real-world scenarios like billing, calculating interest, or simplifying large sets of data.

Importance of Higher Decimal Places

As you move further to the right of the decimal point, each subsequent place represents a smaller and smaller fraction of the whole. While tenths, hundredths, and thousandths are the most commonly encountered place values, it’s important to understand that the decimal system extends infinitely. This means that you can express extremely small quantities with incredible precision using more decimal places. For example, in scientific fields such as chemistry, physics, and astronomy, numbers are often expressed to several decimal places to capture the precise measurements needed for calculations. A number like 0.000001 (one millionth) is small, but in contexts like measuring atomic distances or calculating gravitational forces, these small decimal values are critical for accuracy.

Even in financial markets, decimals are used to express very small price changes. In stock trading, for instance, prices often fluctuate by fractions of a cent, and these tiny variations can have significant impacts on trades and profits. Currency exchange rates also involve small decimal values that can make a big difference in large-scale transactions. Understanding how to interpret and use higher decimal places enables professionals in various fields to work with complex data and ensure accuracy in their work. Thus, mastering decimal place values is essential for both everyday applications and specialized industries that require precision and attention to detail.

Rules of Decimals

Addition and Subtraction of Decimals

When adding or subtracting decimals, the most crucial rule is to align the decimal points. This ensures that each digit is correctly matched with its corresponding place value. For example, when adding 12.34 and 5.6, you would write it as follows, ensuring the decimal points are aligned: 12.34 + 5.60 = 17.94 In this example, 5.6 is treated as 5.60 to facilitate the alignment. After aligning the decimal points, you add or subtract the numbers as you would with whole numbers, carrying over any values as necessary.

If you need to subtract, for example, 5.6 from 12.34, the operation looks like this: 12.34 - 5.60 = 6.74. If there are trailing zeros in the decimal part (like in 5.6), they can be added for clarity during the addition or subtraction but can be omitted in the final result. The importance of aligning decimal points cannot be overstated, as misalignment can lead to significant errors in calculations. Therefore, this rule is foundational in accurately working with decimals in both basic arithmetic and more complex mathematical operations.

Multiplication of Decimals

The rule for multiplying decimals is straightforward: you multiply the numbers as if they were whole numbers and then count the total number of decimal places in both factors to determine where to place the decimal point in the result. For instance, if you want to multiply 2.5 by 1.4, you first ignore the decimal points and multiply as if they were whole numbers:

25 x 4 = 100
25 x 10 = 250
250 + 100 = 350

So, 25 x 14 = 350. Next, you need to determine the number of decimal places in the factors. The first number (2.5) has one decimal place, and the second number (1.4) also has one decimal place, making a total of two decimal places. Therefore, you place the decimal point two places from the right in the product, giving you:

2.5 x 1.4 = 3.50 or 3.5

This rule emphasizes that understanding decimal placement is crucial, as it ensures that the resulting product accurately reflects the values being multiplied. In practical applications such as calculating prices or areas, proper multiplication of decimals ensures that results are both correct and meaningful.

Division of Decimals

Dividing decimals can initially seem more complex, but it follows a systematic approach. The key rule is to eliminate the decimal point from the divisor (the number you are dividing by) by multiplying both the divisor and the dividend (the number being divided) by the same power of 10. This means you shift the decimal point in both numbers to the right until the divisor becomes a whole number. For example, when dividing 3.6 by 0.12, you first convert 0.12 into a whole number by shifting the decimal point two places to the right, making it 12. You must also shift the decimal point in 3.6 the same number of places, converting it to 360. Now your division looks like this:

360 / 12 = 30

Therefore, 3.6 / 0.12 = 30. This process of adjusting the decimal points ensures accuracy in division by removing the complications that decimals can introduce. The rule illustrates how flexibility in working with decimal values can simplify calculations while maintaining their correctness.

Rounding Decimals

Rounding decimals is a critical skill that allows you to simplify numbers while maintaining their approximate value. The basic rule for rounding is to look at the digit immediately to the right of the place value you are rounding to. If this digit is 5 or greater, you round up by adding one to the digit in the place value you are rounding to. If it is less than 5, you simply leave the rounding digit unchanged.

For example, if you want to round 3.678 to two decimal places, you look at the third decimal place, which is 8 (greater than 5). Therefore, you round up the second decimal place (7) to 8, resulting in 3.68. Conversely, if you were rounding 3.672 to two decimal places, the third decimal (2) is less than 5, so you would leave the 7 unchanged, resulting in 3.67. This rule is particularly important in various fields such as finance, engineering, and science, where precision is necessary, but excessive detail can be unwieldy. Rounding helps streamline information without sacrificing too much accuracy, making it easier to communicate results or make decisions based on numerical data.

Converting Between Decimals and Fractions

Converting between decimals and fractions is an essential rule in understanding and working with both forms of numerical representation. To convert a decimal to a fraction, you identify the place value of the last digit. For example, if you have the decimal 0.75, you recognize that 75 is in the hundredths place, which gives you the fraction 75/100. This fraction can then be simplified by finding the greatest common divisor (GCD) of the numerator and the denominator. In this case, both 75 and 100 can be divided by 25, resulting in 3/4.

Conversely, to convert a fraction to a decimal, you divide the numerator by the denominator. For instance, converting 3/4 to a decimal involves performing the division 3 / 4, which results in 0.75. This conversion is crucial for various applications, such as comparing values, performing calculations, or presenting data in a more intuitive format. Understanding how to navigate between decimals and fractions enhances your mathematical fluency and allows for greater flexibility in problem-solving across different contexts, whether in academics or real-world scenarios.