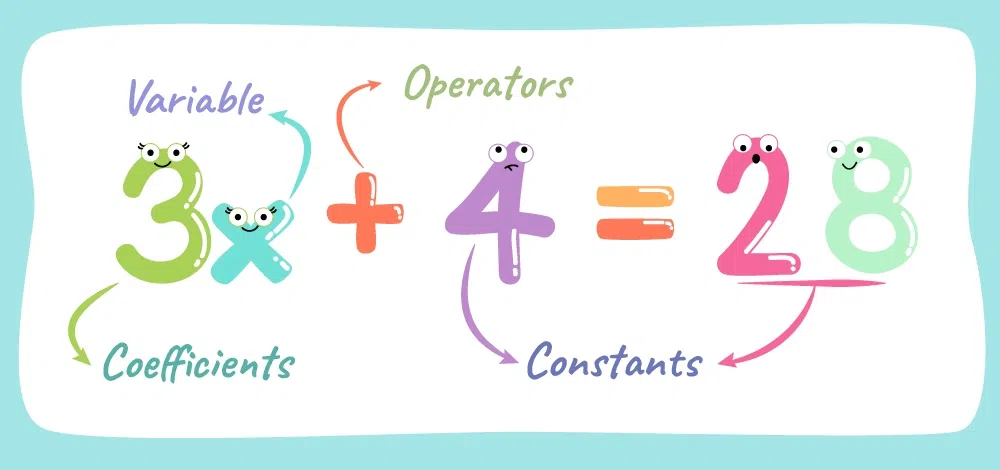
What is Expression?
In mathematics, an expression is a combination of numbers, variables, and operators (such as addition, subtraction, multiplication, and division) grouped together to represent a specific value or relationship. Unlike an equation, which shows equality between two expressions with an equal sign, a mathematical expression does not contain an equal sign. Instead, it is a phrase that represents a value based on the operations performed on its components. Expressions can be as simple as a single number or more complex, involving multiple variables and operations. They are used to describe relationships, simplify calculations, and represent problems that can be solved by applying algebraic rules.
2x + 7
In this expression, x is a variable, and the expression involves multiplying 2 by x, then adding 7. The value of this expression depends on the value of x. For example, if x = 3, then:
2(3) + 7 = 6 + 7 = 13
Algebraic expressions like this are commonly used to represent real-world situations, such as calculating cost, distance, or other quantities that vary depending on certain conditions.
Why is it essential to learn Expressions?
Learning mathematical expressions is crucial because they form the foundation of algebra and higher-level math. Expressions allow students to generalize mathematical operations and relationships, providing a way to handle unknown values, known as variables. By understanding expressions, students can solve more complex problems and prepare for advanced topics such as equations, inequalities, functions, and calculus. For example, an expression like 3x + 5 teaches how to manipulate variables, which is a key concept in all advanced math topics. Algebraic manipulation—simplifying, expanding, or factoring expressions—is essential for problem-solving, not just in academics but in real-world applications like engineering, economics, and physics. Therefore, mastering expressions is the first step toward understanding a wide range of mathematical concepts, allowing learners to think abstractly and logically. Mathematical expressions also help develop logical thinking skills. When learning to manipulate expressions, students are required to follow specific rules and steps, which strengthens their ability to think methodically and carefully. This process enhances their analytical skills, which are essential not only in math but in any field that requires structured problem-solving. Moreover, understanding expressions allows students to recognize patterns and relationships in mathematics, helping them to break down complex problems into manageable parts. This foundational knowledge is key to success in more complex subjects and real-life applications, such as computer programming and scientific research.
Another important reason to learn expressions is their ability to model and simplify real-world problems. Mathematical expressions allow us to represent situations concisely and efficiently, making complex problems easier to analyze and solve. Whether it's calculating profit in business, determining distance in physics, or analyzing data in economics, expressions are an essential tool. For example, in finance, an expression like 500 + 0.03x can represent a scenario where a $500 base salary is combined with a 3% commission on sales (x). This type of expression makes it easier to compute earnings based on different sales amounts, providing a practical, straightforward method for problem-solving. In daily life, expressions help simplify routine tasks, such as figuring out travel time, budgeting, or measuring ingredients in a recipe. Instead of calculating individual components separately, expressions condense the information into a manageable form, making it quicker and more efficient to find the solution. For instance, if you are doubling a recipe, you can represent the change in ingredients with an expression like 2(x), where x represents the original quantity. Understanding how to create and manipulate expressions equips individuals to handle various real-world scenarios more effectively, increasing their problem-solving efficiency in both personal and professional contexts.
Learning expressions enhances abstract thinking by encouraging learners to work with symbols and variables that represent unknowns or general quantities. This abstract thinking is not limited to math but can also improve cognitive flexibility in approaching problems from different perspectives. In algebra, for instance, expressions are not tied to specific numbers; they represent general relationships, allowing students to think beyond immediate, concrete values. For example, the expression a2 + b2 is a general formula that can be used in various scenarios, such as finding the lengths in a right triangle (Pythagoras' theorem). This ability to generalize helps learners think critically and adapt to various situations, whether in science, technology, or everyday problem-solving. Moreover, expressions provide a flexible framework for approaching mathematical problems in multiple ways. When solving for unknowns or analyzing trends, different strategies might apply. By learning how to work with expressions, students gain the flexibility to explore different methods, whether by substitution, factoring, or using technology such as graphing calculators. This flexibility fosters a deeper understanding of the problem-solving process, allowing learners to navigate challenges in creative and adaptable ways. In the professional world, this kind of thinking translates to the ability to innovate, strategize, and approach challenges with a toolkit of flexible methods, ensuring that solutions are found even when the path is not immediately clear.
Rules of Expressions
Simplifying Expressions
One of the most fundamental rules when working with mathematical expressions is simplification. Simplifying an expression means reducing it to its most basic or simplest form without changing its value. This process involves combining like terms, which are terms that have the same variables raised to the same powers, and performing basic arithmetic operations. For example, in the expression 3x + 5 + 2x - 7, the like terms are 3x and 2x, and the constants are 5 and -7. To simplify, you combine the like terms:
(3x + 2x) + (5 - 7) = 5x - 2
The simplified expression is 5x - 2. This rule is essential because it makes the expression easier to understand and work with, especially when solving equations or performing further calculations. Simplifying expressions is a critical step in both algebraic manipulation and higher-level math, allowing for a clearer interpretation of mathematical relationships. Simplification also helps in making complex expressions more manageable. When dealing with large equations or systems of equations, reducing each expression to its simplest form allows you to see patterns, relationships, and potential solutions more clearly. For instance, in calculus or physics, complex formulas often need to be simplified to interpret the results effectively or apply them to real-world problems. This rule encourages a systematic approach to handling expressions, ensuring that calculations are done in the most efficient and accurate way possible.
Expanding and Factoring Expressions
The distributive property is a key rule in handling expressions, especially when multiplication is involved. This rule states that for any numbers or variables a, b, and c, the expression a(b + c) can be expanded as ab + ac. In other words, you distribute the multiplication over the addition or subtraction inside the parentheses. For example, the expression 3(x + 4) can be expanded as follows:
3(x + 4) = 3x + 12
Here, the 3 is multiplied by both x and 4, yielding 3x + 12. This rule is particularly important because it allows us to rewrite expressions in a different form, often making them easier to solve or manipulate. The distributive property is also useful when factoring expressions, the reverse process of expansion. For instance, if you have 6x + 12, you can factor it as 6(x + 2) by pulling out the common factor of 6. The distributive property plays a vital role in algebra, especially when working with polynomials or solving equations. When expressions are expanded, they often become easier to combine with other expressions or integrate into larger problems. Similarly, factoring is an important skill in solving quadratic equations or simplifying expressions before applying other mathematical operations. The ability to expand and factor expressions using the distributive property allows for a flexible approach to solving a wide variety of mathematical problems, from basic algebra to more advanced topics.
Replacing Variables with Specific Values
Substitution is another critical rule when dealing with expressions, especially in algebra. This rule involves replacing variables in an expression with specific numerical values to evaluate the expression. For example, if you have the expression 2x + 5 and know that x = 3, you can substitute 3 for x and simplify:
2(3) + 5 = 6 + 5 = 11
This allows you to find the exact value of the expression for a given variable. Substitution is particularly important in real-world applications, where variables represent specific quantities like time, distance, or cost. By substituting known values into an expression, you can calculate precise outcomes or predictions. For instance, in physics, you might substitute values for velocity and time into an expression to find distance traveled. Substitution is also essential when solving equations. Once an equation has been simplified or factored, substitution allows you to check your solution or solve for additional unknowns. For example, after solving for x in one part of an equation, you can substitute that value into another expression to find related quantities. This rule of substitution enables a step-by-step approach to problem-solving, ensuring that calculations are both accurate and logical.
Grouping Similar Elements Together
Combining like terms is another fundamental rule for simplifying expressions. Like terms are terms that contain the same variables raised to the same powers. This rule states that you can only combine terms that share these characteristics. For instance, in the expression 4x2 + 3x + 5 - 2x2 + 7x, the like terms are 4x2 and -2x2, and 3x and 7x. To simplify, combine these like terms:
(4x2 - 2x2) + (3x + 7x) + 5 = 2x2 10x + 5
This rule is important because it helps in reducing the complexity of an expression, making it easier to understand and solve. By grouping similar elements together, you can break down the expression into simpler components that are more manageable. This is especially useful in algebra and calculus, where expressions can often involve many terms and variables. The process of combining like terms is not only about simplifying, but also about ensuring that the expression is in its most interpretable form. For instance, when solving word problems or real-life scenarios, combining like terms allows you to see the relationships between quantities more clearly, which helps in making better decisions or predictions. This rule also plays a crucial role when working with polynomials and solving multi-step equations, where organizing terms properly is essential for reaching a correct solution.
Performing Operations in the Correct Sequence
One of the most important rules when working with expressions is following the correct order of operations. This rule is often summarized by the acronym PEMDAS: Parentheses, Exponents, Multiplication and Division (from left to right), and Addition and Subtraction (from left to right). This rule ensures that everyone solves an expression the same way and gets the same result. For example, in the expression 5 + 3 x (2 + 4)2, you must follow the order of operations:
Paranthese: 2 + 4 = 6
Exponents: 62 = 36
Multiplication: 3 x 36 = 108
Addition: 5 + 108 = 113
The correct answer is 113. If the operations were performed in a different order, you would get a completely different and incorrect result. Following the rule of order of operations is critical not only for simplifying expressions but also for solving equations accurately. It provides a clear and systematic approach, ensuring consistency in mathematical communication and problem-solving. Order of operations is especially important when dealing with more complex expressions that involve multiple layers of operations. For example, in real-world applications like finance or engineering, where calculations can be intricate, adhering to the correct order of operations ensures that solutions are reliable and accurate. This rule is a universal standard in mathematics, guiding both simple and advanced calculations.
Quiz
1. How did the Hubble Deep Field observation in 1995 change our understanding of the universe?
2. Describe one contribution of ancient Babylonians to early astronomy.
3. Explain the impact of the Islamic Golden Age on the development of astronomy during the medieval period.
4. How did the heliocentric model proposed by Copernicus revolutionize our understanding of the solar system?
5. What are some of the key research areas in contemporary astronomy, and why are they significant?