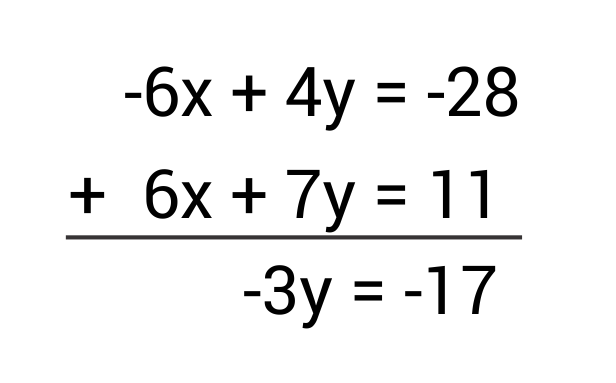What is System of Equations?
A system of equations consists of two or more equations with the same set of unknowns (variables). The goal when solving a system of equations is to find the values of the variables that satisfy all of the equations simultaneously. The system can consist of linear equations, quadratic equations, or more complex forms, but the most commonly studied systems are those made up of linear equations. A system of equations can have: one solution, no solution, infinitely many solutions.
For instance, a simple system of two linear equations with two variables can be written as:
2x + 3y = 6
4x - y = 5
Here, x and y are the unknowns, and we need to find the values of x and y that satisfy both equations simultaneously.
Why is it essential to learn System of Equations?
One of the most important reasons to learn systems of equations is their ability to model and solve real-world situations involving multiple variables. In many complex scenarios, more than one factor influences the outcome, and a system of equations helps to represent these relationships mathematically. For example, in economics, businesses need to balance supply and demand, which can be modeled using a system of equations. Similarly, in physics, multiple forces acting on an object can be described through systems of equations to find unknown variables such as velocity or acceleration. Learning how to create and solve these systems enables us to address practical problems in diverse fields like engineering, finance, chemistry, and biology. For instance, determining the point where two companies break even in terms of costs and revenues might require solving a system of equations where the first equation models cost and the second models revenue.
Another critical reason to learn systems of equations is that they help sharpen analytical and problem-solving skills. Solving a system of equations requires a logical, step-by-step approach that often involves multiple methods, such as substitution, elimination, or graphical representation. Mastering these techniques enhances a student’s ability to think critically, break down complex problems, and apply appropriate strategies to find solutions. For example, a typical system of equations might involve several steps, such as isolating variables, simplifying expressions, and checking the consistency of solutions. This structured process of tackling problems is an essential skill that translates into many areas of life and work, where complex issues must be understood from multiple angles and solved systematically.
Understanding systems of equations is also fundamental for learning more advanced topics in mathematics and science. Systems of equations serve as the groundwork for subjects like linear algebra, calculus, and differential equations, which are essential in fields such as engineering, physics, economics, and data science. In linear algebra, for example, systems of equations are expanded to matrix form to solve more complex problems involving many variables. In calculus, systems are used to understand multivariable functions and optimize them in fields like optimization theory and machine learning. Learning systems of equations provides a solid mathematical foundation that is crucial for anyone pursuing careers in STEM (Science, Technology, Engineering, and Mathematics) disciplines, as well as for understanding more complex scientific phenomena like chemical reactions and population dynamics.
Solutions
Unique Solution
A unique solution occurs in a system of equations when there is exactly one set of values for the variables that satisfies all equations simultaneously. This typically happens when the graphs of the equations intersect at a single point, meaning the lines (in two dimensions) or planes (in three dimensions) cross at only one place. In mathematical terms, the system is consistent and independent because each equation provides a distinct piece of information about the variables.
For example, consider the following system of two linear equations:
2x + y = 5
x - y = 1
To solve this, we can use the substitution method. From the second equation, we can express x in terms of y:
x = y + 1
Substituting this into the first equation:
2(y + 1) + y = 5
Simplifying:
2x + 2 + y = 5
3y = 3 -> y = 1
Now substitute y = 1 back into the expression for x:
x = 1 + 1 = 2
Thus, the solution to the system is x = 2 and y = 1, which is a unique solution. This means that the two lines representing the equations intersect at exactly one point: (2,1). Systems with unique solutions are common in real-world problems where a clear, definite answer is needed, such as determining the exact intersection of supply and demand in an economic model.
No Solution
A system of equations has no solution when the equations represent parallel lines or planes that never intersect. This occurs when the lines have the same slope but different intercepts, meaning they run in the same direction but never meet. In such cases, the system is considered inconsistent because no single set of values satisfies both equations at the same time.
For example, consider the system:
3x - 2y = 6
3x - 2y = 8
Both equations have the same slope (3x - 2y), which means the lines they represent are parallel. However, their right-hand sides are different (6 and 8), meaning they have different y-intercepts. Since parallel lines never intersect, there is no point that satisfies both equations. Therefore, this system has no solution. Graphically, no solution systems are visually represented by two lines that do not touch, symbolizing the fact that there is no common point where both equations are true at the same time. In real-world contexts, no solution might represent conflicting conditions or constraints that cannot be simultaneously satisfied, such as trying to meet two contradictory goals in project planning.
Infinitely Many Solutions
A system of equations has infinitely many solutions when the equations represent the same line or plane, meaning they overlap completely. In such cases, every point on the line or plane is a solution to both equations. Mathematically, this happens when the equations are equivalent, or one equation can be derived from the other through simple algebraic manipulation. This situation indicates that the system is consistent and dependent, as the equations do not provide distinct, independent information.
For example, take the system:
x + 2y = 6
2x + 4y = 12
If we divide the second equation by 2, we get:
x + 2y = 6
This shows that the two equations are identical, meaning they describe the same line. Therefore, every point that lies on this line is a solution to the system. This results in infinitely many solutions, as there are countless points on a line. Graphically, the two equations would appear as the same line on a graph, overlapping completely. In real-world applications, infinitely many solutions might arise when a system represents redundant information, such as multiple measurements of the same relationship. For instance, in physics, it could describe a situation where different methods of measurement confirm the same result, or in economics, it could represent a supply curve and demand curve that perfectly overlap under certain conditions.
Quiz
1. How did the Hubble Deep Field observation in 1995 change our understanding of the universe?
2. Describe one contribution of ancient Babylonians to early astronomy.
3. Explain the impact of the Islamic Golden Age on the development of astronomy during the medieval period.
4. How did the heliocentric model proposed by Copernicus revolutionize our understanding of the solar system?
5. What are some of the key research areas in contemporary astronomy, and why are they significant?