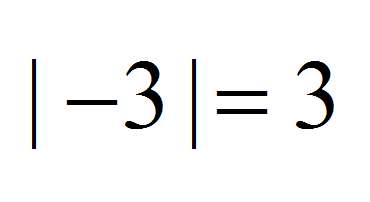What is absolute value?
The absolute value of a number is its distance from zero on a number line, regardless of direction. It is always a non-negative number.
Properties of absolute values:
-
Non-negativity: The absolute value of any real number x is always greater than or equal to zero. No matter if x is positive, negative, or zero, the absolute value will never be negative. It represents distance, and distance cannot be negative.
- | 3 | = 3
- | -3 | = 3
- | 0 | = 0
-
Identity: The absolute value of x is x itself if x is greater than or equal to zero. When a number is already positive or zero, its distance from zero is just the number itself.
- If X = 5, then | 5 | = 5
- if X = 0, then | 0 | = 0
-
Symmetry: The absolute value of −x is the same as the absolute value of x. Both positive and negative numbers are equally far from zero. For example, 5 steps to the right and 5 steps to the left both cover a distance of 5 units.
- | -5 | = 5
- | 5 | = 5
-
Triangle Inequality: The absolute value of the sum of two numbers x and y is less than or equal to the sum of their absolute values. This property tells us that the direct route (adding x and y first) is never longer than taking each step separately and then adding the distances. It essentially states that going directly to your destination is the shortest path.
- | 3 + (- 4) | = | - 1 | = 1
- | 3 + | - 4 | = 3 + 4 = 7
- | 3 + (- 4) | ≤ | 3| + | - 4| = 1 ≤ 7
-
Multiplicative Property: The absolute value of the product of two numbers x and y is equal to the product of their absolute values. When you multiply two numbers, whether they are positive or negative, the distance from zero (absolute value) of the product is the same as multiplying their individual distances.
- | 3 x -2 |= | - 6| = 6
- |3| x |-2| = 3 x 2 = 6
|5|
-
|-3|
=
?
5
+
3
=
8
|12|
÷
|-3|
=
?
12
÷
3
4
The absolute value of a number is its distance from zero on a number line, regardless of direction. It is always non-negative.
Example #1
-
Identify the Absolute Values:
Determine the absolute value of each number.
- | 5 | = 5
- | -3 | = 3
-
Substitute the Absolute Values: Replace the original numbers with their absolute values.
- | 5 | + | -3 | = 5 + 3
-
Perform the addition and get final result: Add the absolute values together.
- 5 + 3 = 8
- The final result is 8
Example #2
-
Identify the Absolute Values:
Determine the absolute value of each number.
- | 12 | = 12
- | -3 | = 3
-
Substitute the Absolute Values: Replace the original numbers with their absolute values.
- | 12 | ÷ | -3 | = 12 ÷ 3
-
Perform the addition and get final result: Add the absolute values together.
- 12 ÷ 3 = 4
- The final result is 4
Quizzes:
1. John walks to a park located 6 miles east of his house and then walks back home. What is the total distance John walks in a round trip?
2. A thermometer indicates a temperature of − 5*C. What is the actual temperature, considering absolute values?
3. A submarine dives to a depth of −250 meters below sea level. What is the absolute depth of the submarine underwater?
4.A hot air balloon rises 200 meters above ground level. Later, it descends 150 meters. What is the total change in altitude, considering absolute values?
5.A bank account has a balance of −$50. What is the absolute value of the debt?